Pythagoras

Pythagoras van Samos leefde in de zesde eeuw v. Chr. (geboren rond -580 op het eiland Samos, gestorven rond -500 in de Zuid-Italiaanse stad Metapontum). Omstreeks -532 emigreerde hij naar Croton in Magna Graecia, waar hij een filosofisch-religieuze gemeenschap stichtte, waarvan de leden een opvoeding genoten die hen ook in staat moest stellen om een rol te spelen in de politiek van hun stad. Onderwijs in de wiskunde nam er een belangrijke plaats in. De aandacht voor wiskunde en voor het verwerven van politieke invloed vertonen verwantschap met de werking van Plato's Academie. Het is daarom niet verwonderlijk dat Plato veel belangstelling had voor de Pythagoreïsche filosofie, mede door zijn contacten met de wiskundige Archytas uit Tarente. Via de Academie kreeg ook Aristoteles belangstelling voor de denkbeelden van Pythagoras.

Het doel van de filosofie van Pythagoras is de goddelijke harmonie van het heelal te doorgronden, waar alles terug te brengen is tot getallen. Hij ontdekte ook dat de muziek aan getallen onderworpen is. In zijn wereldbeeld zijn de planeten goddelijke, levende en redelijke wezens die volgens regels hun cirkels in het heelal doorlopen. De astronomie moet die regels ontdekken door te steunen op de wiskunde.

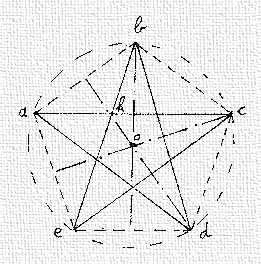
Het pentagram was het heilteken van zijn gemeenschap. Indien we telkens een hoekpunt overslaan vormen de overblijvende hoekpunten van een pentagram een regelmatige vijfhoek (onze punten a, b, c, d en e). Om de figuur te construeren met passer en lineaal verwijzen we naar deze handleiding en naar een alternatief. Om een regelmatige vijfhoek te construeren indien de zijde gegeven is, is er deze werkwijze. Indien we de gewenste zijde van de vijfhoek gelijkstellen aan 5, zal de straal van de omschrijvende cirkel zijn:
r = ^z⁄ _{√(5-√5)⁄2}

De loodlijnen vanuit de punten b, c en d op de tegenoverliggende zijden van de vijfhoek snijden mekaar in het middelpunt van de cirkel die de vijfhoek juist omschrijft (om redenen van overzichtelijkheid hebben we de loodlijnen vanauit a en e niet afgebeeld).

De combinatie van de gelijkzijdige driehoek met basis |ac| en de driehoek bed zonder basis lijnt het pentagram af. Vergelijk met:

We trekken vervolgens de diagonalen |ac|, |be|, |bd|, |ce| en |ad|. Zij snijden mekaar volgens de gulden snede.

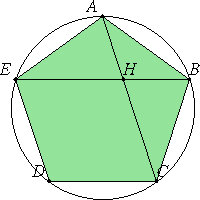
Daarvan vinden we het wiskundige bewijs in boek 13, stelling 8 van Euclides. Op basis van eerdere stellingen inzake gelijkbenige driehoeken en de gelijkvormigheid tussen driehoeken wordt tussen de diagonalen en de gelijke zijden van de vijfhoek de verhouding van de gulden snede bewezen. In de volgende figuur kunnen we de gelijkheid van de hoeken in de driehoeken AEB en ABC ook ontdekken door te onthouden dat de som van de hoeken in een driehoek altijd 180° is en de hoeken van een regelmatige vijfhoek hoeken van 108° zijn. EAH is een gelijkbenige driehoek en daarin is het langste stuk van de diagonaal (EH) gelijk aan de zijde EA en dus ook aan de zijde AB (de vijf zijden van een regelmatige vijfhoek zijn gelijk). De verhouding tussen basis EB (diagonaal) en AB (zijde) is gelijk aan die tussen AB als basis en HB (kortste stuk van de diagonaal en zijde van de gelijkbenige driehoek ABH), aan die tussen EB en EH en aan die tussen EH en HB, steeds volgens de gulden snede.

Om de middelevenredigheid volgens de gulden snede te berekenen: het grootste deel van het lijnstuk verhoudt zich tot de totale lengte als het kleinste zich verhoudt tot het grootste. Stellen we de totale lengte |ac| voor door x, het langste stuk |kc| door y en het kortste |ak| door z - in hun algebraïsche bewerkingen verkozen de Griekse wiskundigen te werken met lijnstukken en meetkundige figuren (zie ook het Delische probleem of de verdubbeling van de kubus).
Dan kunnen we schrijven x ÷ y = y ÷ z of y² = x × z. Als de totale lengte x = 5, hebben we te maken met twee onbekenden.
We kunnen z echter ook omschrijven als 5 - y.
Via y² = 5(5 − y) bekomen we tenslotte een vierkantsvergelijking van de gedaante ax² + bx + c = 0:
y² + 5y − 25 = 0

De oplossing hiervoor is:
(−b + √Δ) ÷ 2a met
Δ = b² − 4ac of 25 + 100 = 125
wat ons tenslotte brengt tot: (-5 + √125) ÷ 2 = 3,09017

Het langste deel is dus 3,09 cm, het kortste 1,91 cm. Als we de totale lente gelijkstellen aan 1, dan is de verhouding totale lengte ten opzichte van het grootste deel 1/[(1 + √5) ÷ 2] of 2 ÷ (1 + √5).

De breuk (1 + √5) ÷ 2 is de gulden snede 1,618034 (Grieks symbool: Φ) die in de architectuur bekend staat als modulor (samentrekking van module en section d' or). Algemeen is immers Φ = a ⁄ b = (a + b) ⁄ a = a ⁄ a + b ⁄ a = 1 + b ⁄ a = 1 + 1 ⁄ Φ.
⇔ Φ + 1 = Φ²
⇔ Φ² - Φ - 1 = 0. Deze vierkantsvergelijking kunnen we oplossen zoals hierboven.
Delen we 5 (de totale lengte van een lijnstuk in ons pentagram) door de gulden snede, bekomen we ook de uitkomst 3,09.

Buiten zijn beroemde stelling nam de Griekse meester ook de gulden evenredigheid over van de Babyloniërs:

A ÷ H = R ÷ B met H = 2AB ÷ (A + B) en R = (A + B) ÷ 2

Toegepast op de afmetingen van het Parthenon, A = 69,5 meter en B = 30,9 meter, geven zowel A ÷ H als R ÷ B als uitkomst 1,624 of bij benadering de gulden snede! Indien we de volledige formules van H en R in de vergelijking invoegen en volledig uitwerken, blijkt dat de halve omtrek en de dubbele breedte zich middelevenredig verhouden: (A + B) ÷ 2B = 1,624