De verdubbeling van de kubus

De verdubbeling van de kubus is, naast de kwadratering van de cirkel en de trisectie van een hoek, een wiskundig probleem dat gedurende de hele klassieke Oudheid de volle aandacht genoot van de bekendste Griekse wiskundigen. Die vermoedden reeds dat dit probleem niet op te lossen valt met passer en (ongemerkte) lineaal. Traditioneel begint elke beschrijving met het verhaal van de inwoners van het eiland Delos, die het orakel van Delphi bevragen hoe ze een einde kunnen laten stellen aan de pestepidemie die hun eiland teistert. Volgens het orakel dienden ze een kubusvormig altaar van de god Apollo te verdubbelen zonder de vorm te wijzigen. Volgens het verhaal togen de Deliërs vol goede moed aan het werk en verdubbelden alle ribben, waardoor ze wel de kubusvorm behielden maar het volume verachtvoudigden, wat niet de bedoeling was. De epidemie verergerde. Uiteindelijk wonnen ze de raad in van Plato. Maar wanneer? Dikwijls verwijzen moderne commentatoren naar de pestepidemie die Athene in 430 trof, maar op dat ogenblik was Plato nog niet geboren. Bovendien vinden we al een spoor van het probleem van de kubusverdubbeling bij een wiskundige die een generatie eerder leefde, Hippocrates van Chios, niet te verwarren met die van Kos (die zijn naam gaf aan de eed voor artsen). Hippocrates van Chios heeft zelf geen bewezen oplossing gegeven (of ze is niet bewaard gebleven), maar wel aangegeven in welke richting de wiskundigen na hem dienden te zoeken: het vinden van tweede middelevenredigen tussen 1 en 2, zodat 1 ⁄ ³√2 = ³√2 ⁄ (³√2)² = ³√2² ⁄ 2, of, in decimale notatie 1 ⁄ 1,2599 = 1,2599 ⁄ 1,5827 = 1,5827 ⁄ 2.

Voor ons lijkt de oplossing niet zo moeilijk. Stel dat de oorspronkelijke kubus een ribbe heeft van 1 meter, dan is het volume 1³, het dubbele daarvan is twee en de ribbe van die tweede kubus is dus de derde vierkantswortel van 2 of ³√2 (bij benadering 1,2599...). Met een rekenmachine of een rekenblad gaat dat heel snel, maar daarover beschikten de Grieken niet. Het berekenen van een derdemachtswortel is immers geen elementaire rekenoperatie zoals optellen of vermenigvuldigen. De uitkomst van de worteltrekking levert ons een irrationaal getal op, dat we per definitie nooit exact in decimale notatie kunnen weergeven. Tot hun afgrijzen hadden de Pythagoriërs ontdekt dat ze de vierkantswortel van 2 niet konden noteren als een geheel of rationaal getal, de verhouding van twee gehele getallen. Een rationaal getal in het decimale stelsel heeft achter de komma een eindig aantal cijfers of een zich steeds herhalende rij van 1 of meer cijfers. Daarom noemden ze getallen zoals √2 incommensurabel, onmeetbaar, enkel meetkundig te construeren; zo konden ze √2 voorstellen als de diagonaal van een vierkant met zijde 1. Wij noemen deze getallen nu irrationaal.

Het zou ons te ver leiden om alle oplossingen uit de klassieke Oudheid te bespreken (voor een volledig overzicht: Colin B. P. McKinney, The Duplicators, Part I: Eutocius's Collection of Cube Duplications). De overlevering van die oplossingen hebben we te danken aan Eutocius van Ascalon (480-540). Bij de bespreking van Archimedes' Over bol en cylinder deel 2 botst hij op een derdemachtvergelijking van de gedaante x³ = b²c. Archimedes lost ze op door 2 middelevenredigen tussen b en c te zoeken, maar gaat ervan uit dat die methode door al zijn lezers gekend is en geeft geen verdere uitwerking. Daarom gaat Eutocius er dieper op in, legt het verband met de verdubbeling van de kubus en geeft een historisch overzicht van de oplossingen, elf in totaal. Wie de oplossingen naast elkaar legt, komt tot de vaststelling dat de wiskundigen in de Oudheid veelvuldig een voorliefde hadden voor gelijkvormige driehoeken, kegelsneden en krommen.

Specialisten die zich op dit studiegebied wensen te begeven, dienen zowel begaafde mathematici te zijn als een grondige kennis te hebben van de oude Griekse taal en in het bijzonder van de terminologie van de oude Griekse wiskunde, waarbij ze zich telkens ook moeten afvragen of de bestudeerde Griekse wiskundige over de juiste basiskennis beschikte voor de gereconstrueerde oplossingen, met andere woorden de moderne wiskundigen mogen zich niet bezondigen aan anachronismen.

Het staat wel vast dat de eerste groep wiskundigen die aan het vraagstuk van de verdubbeling van de kubus hebben gewerkt connecties hadden met Plato of zijn Academie. In Plutarchus' werk Quaestiones Convivales, Boek 8, Hoofdstuk 2, Paragraaf 1 (Stephanus 718) vinden we een verwijzing naar Plato die Archytas, Eudoxus en Menaichmos berispt (of onrechtstreeks via hun leerlingen), omdat ze voor hun oplossingen werktuiglijke constructies gebruikten, want zo wordt het goede aan de meetkunde vernietigd en ten gronde gericht, doordat de meetkunde zich weer tot het waarneembare terugwendt in plaats van zich daarboven te verheffen en vast te houden aan de eeuwige, onstoffelijke beelden… Die kritiek is verwonderlijk. De oplossing van Archytas maakt gebruik van bewegende driehoeken en halve cirkels en bespreken we zo dadelijk, die van Eudoxos is spijtig genoeg verloren gegaan, maar waarschijnlijk gebaseerd op krommen en die van Menaichmos, een student van Eudoxos, is gebaseerd op kegelsneden (parabolen en hyperbolen). Hoe de wiskundigen volgens Plato dan wel te werk dienden te gaan, blijft een vraagteken.

Volgens B. L. van der Waerden (Ontwakende wetenschap, Noordhoff, Groningen, 1950 ) heeft Plutarchus geput uit een verloren gegane dialoog van Eratosthenes (die zich als eerste waagde aan het berekenen de omtrek van de Aarde) Platonikos waarin hij de filosofie van Plato uiteenzette, niet door middel van een saai referaat, maar door interactie met een aantal personages die Plato wel degelijk gekend heeft, maar daarom zijn de gedane uitspraken, hoewel niet per se onmogelijk, toch niet eenduidend historisch te noemen.

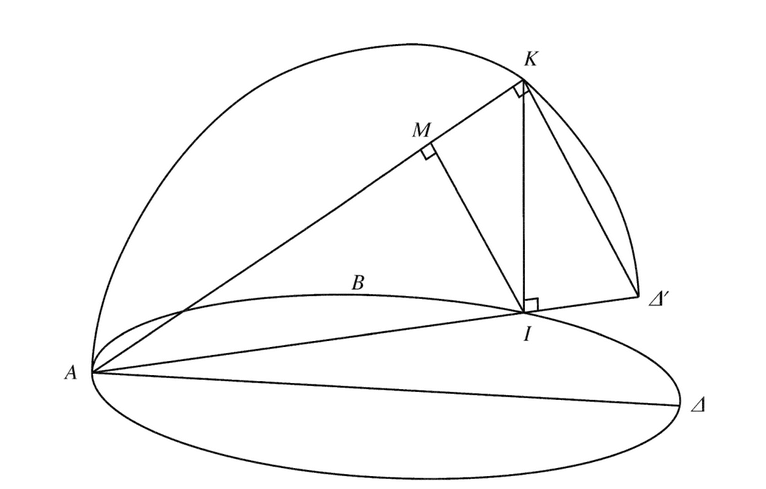
Voor de oplossing van het probleem van de verdubbeling van de kubus doet Archytas beroep op de eigenschappen van gelijkvormige driehoeken. Zo kan hij in een zogenaamde Archytasconfiguratie twee middelevenredigheden construeren. De verhouding liggende zijde-schuine zijde in de driehoeken AMI, AKI en AKD is immers gelijk:
AM ⁄ AI = AI ⁄ AK = AK ⁄ AD. Merk op dat de schuine zijde van de eerste driehoek de liggende zijde is van de tweede en de schuine zijde van de tweede de liggende zijde van de derde.

In een evenredigheid is het product van de uiterste termen gelijk aan het product van de middelste termen, dus: (AI)² = AM × AK; in een gedurige evenredigheid met drie ratio's is ook AM × AD = AI × AK of
AK = AM × AD ⁄ AI.
De eerste gelijkheid wordt dan: (AI)² = AM × AM × AD ⁄ AI. We kunnen nu AI overbrengen naar het andere lid, waardoor we een derde kwadraat verkrijgen: (AI)³ = (AM)² × AD. AI en AK zijn dus de gezochte middelevenredigen.

Ramon Masià heeft op Geogebra de oplossing van Archytas gereconstrueerd in twee stappen. Om de voorgaande tekst het best te illustreren beginnen we met constructie 2. De beginsituatie beelden we hieronder links af. Door met de muis K te bewegen over de halve cirkel ontvouwt zich de hierboven beschreven configuratie (de animatie werkt niet op onze website, gebruik de link!). Rechts staat de eindsituatie met de gelijkvormige driehoeken.

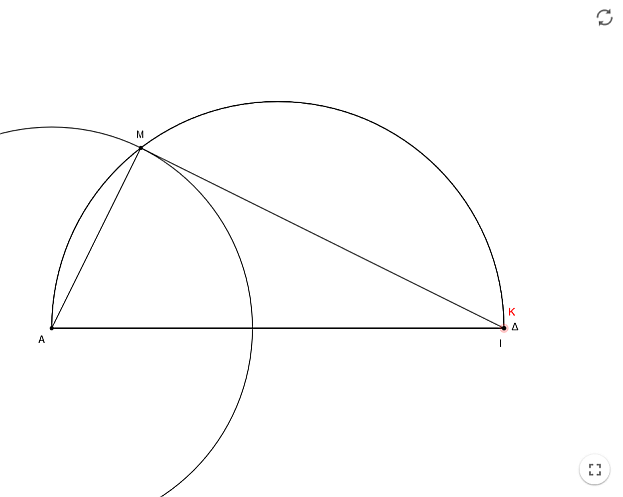
Om tot een Archytasconfiguratie te komen, dienen volgende voorwaarden voldaan:

• ⇒ het punt K ligt in het verlengde van het gegeven lijnstuk AM met lengte = 1.
• ⇒ de loodlijn uit de rechte hoek K snijdt het andere gegeven lijnstuk AD met lengte 2 in I, zó, dat KI de halve cirkel, die de rechthoekige driehoek AMI omsluit, raakt in I.
• ⇒ de lijnstukken MI en KD lopen evenwijdig

In de tweede reconstructie beweeg je K op dezelfde manier, maar nu laat Archytas de grote halve cirkel roteren rond A tot I en I' samenvallen. In de animatie wordt de tweede halve, kleine cirkel AMI' niet afgebeeld. Merk op dat de reconstructie tweedimensionaal is. Masià en Colin B. P. McKinney hebben in Geogebra ook driedimensionale modellen gebouwd die de overgeleverde tekst zo accuraat mogelijk volgen. In het oorspronkelijke manuscript staat immers een tweedimensionaal diagram.

Eutocius vermeldt ook een (werktuiglijke) oplossing die hij toeschrijft aan Plato! Blijkbaar was er in de Griekse wereld behoefte aan een apparaat waarmee men middelevenredigheden kon berekenen. Eratosthenes ontwierp zo'n apparaat dat hij mesolabium noemde. De Romeinse auteur Vitruvius vernoemde het met veel lof in het negende boek van zijn De Architectura. Het spreekt vanzelf dat bouwheren en steenhouwers niets konden aanvangen met oplossingen die beroep deden op roterende figuren, krommen en kegelsneden. Later kreeg het mesolabium een tweede leven in de muziekwereld.

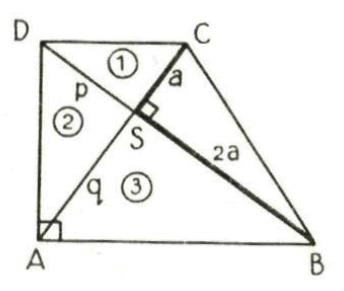
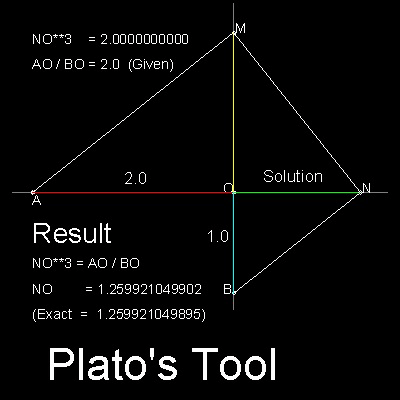
Het apparaat dat Eutocius aan Plato toeschrijft is in spiegelbeeld een trapezium, waarvan de diagonalen loodrecht op mekaar staan. Zo verkrijgen we drie gelijkvormige driehoeken en komen we stapsgewijze tot p³ = 2a³.

Literatuur

• Bos, H. J.M., Redefining Geometrical Exactness. Descartes' transformation of the early modern concept of construction, Sources and Studies in the History of Mathematics and Physical Sciences. Springer-Verlag, New York, 2001
• Huffman, C., "Archytas", The Stanford Encyclopedia of Philosophy (Summer 2018 Edition), Edward N. Zalta (ed.), URL = https://plato.stanford.edu/archives/sum2018/entries/archytas/
• Lattmann, C., Mathematische Modellierung bei Platon zwischen Thales und Euklid, De Gruyter, Berlijn/Boston, 2019
• Little, J. B., A Mathematician Reads Plutarch: Plato's Criticism of Geometers of His Time, Journal of humanistic mathematics, Volume 7, Issue 2, juli 2017
• Menn, S., How Archytas doubled the Cube, in: The Frontiers of Ancient Science: Essays in Honor of Heinrich von Staden, eds. B. Holmes, K-D Fischer, De Gruyter, Berlijn, 2015
• Masià, R., A new reading of Archytas’ doubling of the cube and its implications. Arch. Hist. Exact Sci. 70, 175–204 (2016). https://doi.org/10.1007/s00407-015-0165-9
• O'Connor J. J. and Robertson E. F., Doubling the Cube, MacTutor History of Mathematics, (University of St Andrews, Scotland, april 1999) https://mathshistory.st-andrews.ac.uk/HistTopics/Doubling_the_cube/
• Saito, K., (1995) Doubling the cube: A new interpretation of its significance for early greek geometry. Historia Mathematica - HIST MATH. 22. 119-137. 10.1006/hmat.1995.1013.
• van der Waerden, B. L., Ontwakende wetenschap, Noordhoff, Groningen, 1950